32 o 16 teste di serie. Pericolo negli Slam per i numeri 1, la simulazione

E’ notizia di poche settimane fa che gli Slam a partire dal 2019 torneranno al sistema di 16 teste di serie in vigore prima del 2002. Insomma si tratta di un ritorno al passato che fa storcere il naso a qualcuno. Il passaggio da 16 a 32 seeds era stato accolto come un grande passo in avanti a tutela in primis dei migliori giocatori del mondo e in seconda battuta dello spettacolo. In questo caso è facile intuire che con 32 teste di serie i migliori si possono incontrare solo nella seconda settimana di uno Slam. Tutti sanno come funziona il sistema del seeding a 32, ma meglio ricapitolarlo. In uno Slam entrano nel tabellone principale 128 giocatori, di questi i 32 con il miglior ranking ATP entrano nel lotto delle teste di serie (discorso diverso vale per Wimbledon che non stiamo qui ad approfondire). Questi 32 privilegiati non si possono incontrare prima del terzo turno. Questo vuol dire che nel primo e secondo turno i migliori incontrano molto spesso dei carneadi lasciando così al prosieguo del torneo le sfide tra grandi. Lo schema degli accoppiamenti è il seguente:

1. Al 3T: 1-8 vs 25-32 e 9-16 vs 17-24
2. Al 4T: 1-4 vs 13-16 e 5-8 vs 9-12
3. Ai QF 1-4 vs 5-8
4. In SF 1-2 vs 3-4
5. In F 1-2

La soppressione delle tds 17-32 non fa altro che annullare la riga 1, lasciando invariato lo schema. Questo implica che le tds possono incontrarsi solo dal 4T in poi. Se vogliamo è anche una semplificazione del tabellone (e anche delle simulazioni e della proiezioni). Tradotto in soldoni questo significa che un ipotetico numero 1 del seeding al 1T invece di avere la possibilità di avere un anonimo 33° del ranking (molto spesso, se non sempre maggiore) può ritrovare un 17° uomo certamente più difficile da affrontare del primo.

Queste considerazioni sono molto semplicistiche e facili da dedurre, ma ora facciamo sul serio e proviamo a calcolare in maniera deterministica come un giocatore è penalizzato o meno da questo nuovo – che poi è vecchio – sistema.

Simulazione

Per poter operare ci servono degli strumenti di simulazione. Grazie al prezioso lavoro di Jeff Sackmann abbiamo a disposizione tutto l’occorrente, solo che bisogna saperlo usare. Per poter fare delle proiezioni sui tornei in corso appena dopo la compilazione dei tabelloni Jeff ha implementato un sistema molto efficace. Inutile stare a dilungarci sui dettagli. Per un maggiore approfondimento è opportuno leggere la guida linkata qui. In sintesi si tratta di un metodo Monte Carlo (non c’era il Principato) in cui si lanciano un numero elevato di simulazioni (nel nostro caso saranno 100.000) in cui si fanno scontrare tra loro i giocatori. Il vincitore viene decretato da un numero pseudo-random: se il numero ricade nell’intevallo 1 – JRank1 allora vince il 1° giocatore, se cade nell’intervallo (JRank1+1) – (JRank1+JRank2) allora il vincitore è il 2° giocatore. Attenzione! Facciamo un passo indietro, forse siamo andati un po’ troppo avanti con l’argomentazione e qualcuno si è perso. Innanzitutto dobbiamo dire che cosa è questo “JRank“. Il JRank (per approfondire) è un particolare ranking formulato da Jeff che si basa su quello ATP però ne modifica alcune peculiarità che non staremo qui ad approfondire. Per dirne una: i punti ATP non sono distribuiti in maniera omogenea dalla 52^a settimana passata a oggi, ma si dà un valore maggiore a quelli più vicini al presente e minore a quelli del passato. Non è fondamentale usare il JRank per il nostro goal, si potrebbero usare anche i punti ATP, anch’essi hanno lo stessa efficacia del ranking di Jeff e, aggiungerei, sono unanimamente condivisi. Per renderci conto di come funziona la simulazione di una partita facciamo un esempio pratico. Supponiamo di avere Nadal con 12390 punti JRank e Youzny con 2900 punti. Lancio l’app che mi dà un numero, supponiamo 12000. Bene siccome 12000 è minore di 12390 allora in questo caso vincerà Nadal. Altra simulazione: numero 12400. Qui vince Youzny perché 12400 > JRank1+1. Come è facile intuire Nadal ha molte più probabilità di vincere di Youzny. Iterando l’operazione per tutte le partite turno per turno viene fuori la probabilità di arrivare al turno x e di vincere il torneo.

Fino a qui tutto bene, ma il programma dove lo possiamo trovare? Bene Jeff si prodiga anche di pubblicare il sorgente in Python. E’ possibile scaricare il codice a questo link. Non si sa perché, o perché Jeff non vuole che il suo codice venga usato da inesperti, o perché magari ha usato una versione di Python vecchia, però il codice pubblicato non funziona, ci sono 2 bug che ho corretto, per cui, chi è interessato, può scaricare il codice funzionante da qui (sono necessari anche delle librerie disponibili qui e qui). Abbiamo a disposizione la pistola, però ora sono necessari i proiettili. No problem. Sackmann ha pubblicato pure un esempio di tabellone per le simulazioni, nel caso specifico quello degli Australian Open 2011. Il listato CSV è disponibile a questo link. Ora ci siamo per davvero. Chi è uno smanettone sa come fare partire il programma, chi non lo è si arrangi (o veda il video che ho caricato su Youtube). Non è difficile.

Caso normale

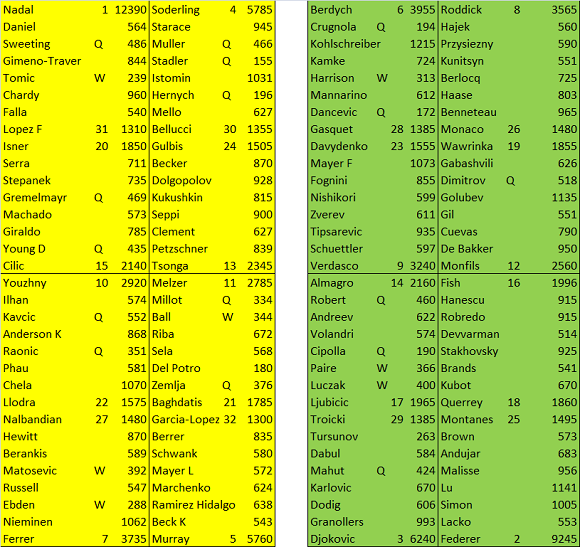
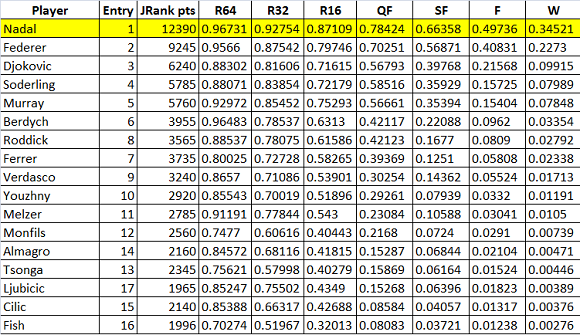
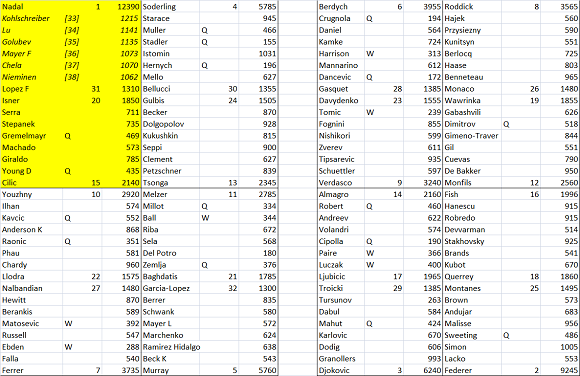
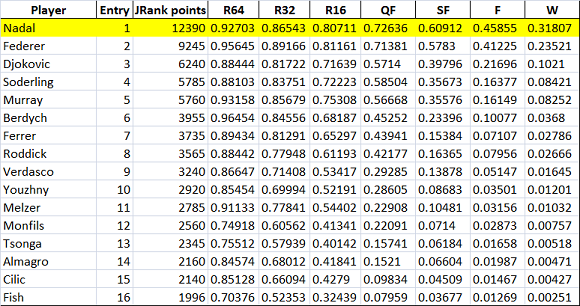
Questo è il caso normale, o reale se preferite, ossia quello che si è verificato per davvero. Il tabellone riportato è diviso in parte alta in giallo e verde quella bassa. A sua volta ogni parte è divisa in 4 spicchi o sezioni. Lanciamo la simulazione e riportiamo i risultati dei primi 16 del seeding.

Nadal ha il 96.7% di probabilità di arrivare al 2T, 92.7% di arrivare al 3T, 87.1% di arrivare al 4T, 78.4% ai QF, 66.3% in SF, 49.7% di arrivare in F e 34.5% di vincere. (Questo è l’output che dovreste avere se sapete far funzionare il programma).

Caso peggiore 16 teste serie

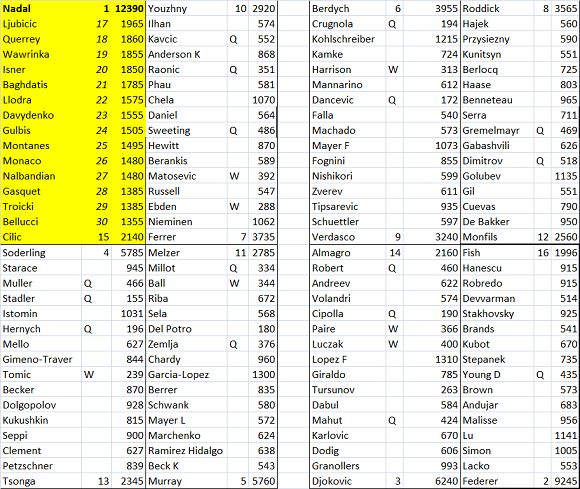
Rimescoliamo il tabellone considerando solo 16 teste serie e assegniamo a Nadal il percorso peggiore possibile, almeno per quanto riguarda il suo spicchio di tabellone. Come già accennato, la prima tds può prendere tutti dalla 17a posizione in giù, così il worst case è fatto da tutti i tennisti che vanno dalla 17^a posizione alla 30^a, caso molto improbabile, ma possibile. Lanciamo di nuovo la simulazione e troviamo i seguenti risultati.

Come era prevedibile Nadal perde punti in tutte le caselle. Drastico è il passaggio del 2T e 3T che nel caso reale, in base ai dati, sembra una formalità. Questo caso però non si può paragonare con quello reale, per renderci conto di quanto siano deleterie le 16 tds per i primi della classe ci serve il worst case a 32 teste di serie.

Caso peggio a 32 teste di serie

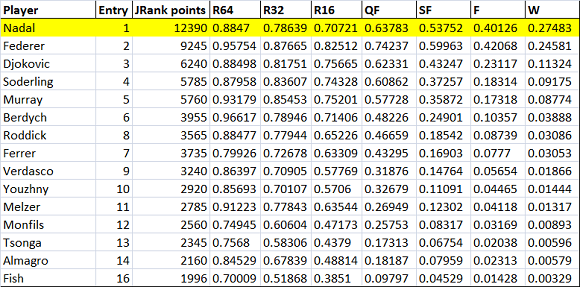
A Nadal piazziamo i giocatori che come JRank vanno dalla 33^a posizione alla 38^a. Facciamo partire la simulazione.

Anche qui i risultati rispecchiano le nostre previsioni. Con 32 teste di serie Nadal ha molte più probabilità di andare avanti così come di vincere il torneo. Per concludere facciamo un confronto tra i 2 worst cases: 16 vs 32 seeds.

Confronto caso peggiore 32 seeds vs 16 seeds

 

Le differenze di percentuali possono sembrare minime, ma un 1% su 128 giocatori è un grandissimo gap. Arrivare al terzo turno per Nadal è  leggermente più difficile, ma lo è per tutti i big quando ci sono 16 e non 32 teste di serie.

Come continuare? Ora che avete imparato il metodo fate partite la simulazione per Federer.

 

Video tutorial per la simulazione