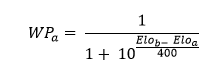The GOAT Theory: Elo Counter

Purtroppo il capitolo precedente della GOAT Theory non ci permette di trovare una proporzione accettabile tra qualsiasi torneo e le ATP Finals o Masters. Il loro formato di singolare poco si addice ad una semplice proporzione, che è necessaria sì, ma non può mai essere trovata con il metodo che ci ha permesso di arrivare a quello tra Slam/M1000/AT500/ATP250. Qui il gioco era facile perché sono tutti tornei ad eliminazione diretta con un tabellone 2ⁿ o comunque 2ⁿ like e soprattutto con la clausola essenziale che un giocatore deve vincere tutte le partite per aggiudicarsi il torneo. Nelle Finals è contemplata anche la possibilità che un giocatore trionfi anche perdendo 3 partite (Se un giocatore gioca 3 partite e le perde tutte però tutti gli altri 3 si ritirano passa lui perché è quello che ha giocato il maggior numero di partite). Non un grande aiuto dal punto di vista dei calcoli. Come risolvere? Spostiamo la prospettiva e chiediamo aiuto alla tanto agognata Elo.

L’idea che sta alla base dell’Elo è che è impossibile misurare la forza di un giocatore in senso assoluto, allora sono i suoi risultati a fargli guadagnare o perdere punti. Si parte da un punteggio base, che per gli scacchi è 1500 e il plus in caso di vittoria dipende dall’avversario battuto. Se l’avversario è più forte, ossia ha una Elo più alta, allora ci sarà un grande guadagno, se l’avversario è meno forte, con Elo inferiore, allora il guadagno sarà inferiore. Stesso ragionamento, ma all’inverso in caso di sconfitta.

Elo Slam

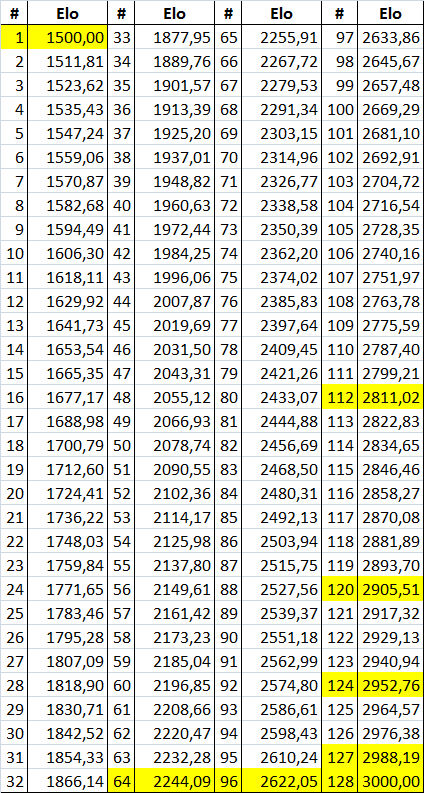
Negli scacchi il giocatore con la Elo di partenza, non la più bassa, ha 1500 punti. Supponiamo che in un tabellone a 128, così com’è negli Slam, l’ultimo tennista nella entry list abbia una Elo di 1500. Purtroppo non esiste una Elo massima che può raggiungere un giocatore. C’è un limite sul secondo in base al quale superato un certo punteggio non si può più acquisire punti, ma questo dipende dal distacco del numero 1 dal numero 2, quindi non si può applicare. Allora per toglierci dall’empasse supponiamo che chi sta più in alto di tutti abbia una Elo di 3000, ossia il giocatore 127 posizioni avanti al primo con Elo che ne ha 1500 ha Elo uguale a 3000, e chi sta 127 posizioni dietro ne ha 0.

Abbiamo così 2 estremi: 1 a 1500 e l’altro a 3000. Distribuiamo in maniera omogenea la Elo: (3000 – 1500) / 128 = 11.71875. Ad ogni scatto in graduatoria un giocatore della entry si acquista 11.71875 punti Elo. Calcoliamo la Elo media di un partecipante che è di 2250 punti e facciamo partire la simulazione.

Sappiamo benissimo che un giocatore medio, quindi non testa di serie, può incontrare chiunque nel corso di uno Slam, ma per semplicità si suppone che incontri giocatori sempre più forti fino alla finale. Nel primo turno incontrerà un giocatore con media dall’1 al 65 che è uguale a 1877.95, nel secondo turno un giocatore dal 66 al 97, 2450.79. Terzo turno dal 98 al 113 con Elo 2734.25. Quarto turno dal 114 al 121, 2875.98. Quarti di finale 122-125, 2946.85. Semifinali 126-127, 2976.38. Finale con il 128: 3000.

Date 2 Elo la Winning Probability è data dalla formula:

 

 

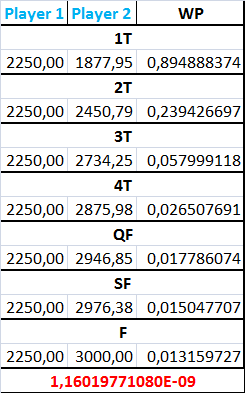
Iterando la formula per i 7 turni utili per vincere uno Slam si hanno i seguenti risultati:

La WP di vincere uno Slam per un giocatore con Elo media è di 1.16 * 10^-9. Come già successo in passato, qui i concetti di probabilità di vincere con la difficoltà di vincere si mescolano, per cui è meglio considerarli coincidenti per comodità.

Elo Masters

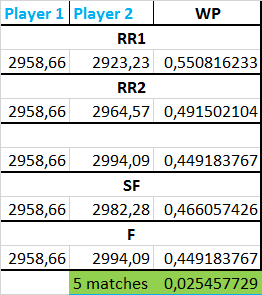
A questo punto sembra scontato il passo successivo. Dei 128 giocatori partecipanti ad un torneo dello Slam si selezionano i migliori 8, così come avviene in linea teorica per il torneo di fine anno, e si fanno scontrare tra loro secondo la formula del round robin a 2 gironi con semifinali e finale. Anche in questo caso il giocatore che dovrà affrontare le 3 partite del girone + le 2 a eliminazione diretta sarà il giocatore medio, medio secondo la Elo di tutta l’entry list che in questo caso è pari a 2958.66. Il giocatore medio affronta nel 1^a partita del RR uno con la media del 7°-8°, con Elo di 2923.23, poi nella 2^a uno con media 3°-4°-5°, questo perché la media lo colloca nel mezzo tra 4° e 5° giocatore, e nell’ultima partita del RR, la più difficile, quella con la media del 1°-2°. Lo scontro in semifinale sarà con un giocatore la cui Elo sarà la media dei primi 4 partecipanti e la finale con la media dei primi 2. Considerando per assodato che il giocatore selezionato vinta tutt’e 5 le partite i dati in nostro possesso evidenziano questi risultati:

La probalità di vincere il Masters diventa di 0.025457729 che sembrerebbe un numero molto basso, però se confrontato con 1.16 * 10^-9 dello Slam si ha un rapporto di 21.942.577 a favore dello Slam. Un numero esorbitante che però rendere l’idea di quanto sia molto più difficile vincere uno Slam rispetto al Masters di fine anno.

Elo Reale Slam

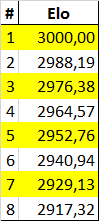
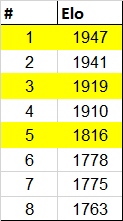
Forse le proiezioni ideali sono troppo distanti dalla realtà. E in effetti i dati week-by-week ci restituiscono dei valori che sono completamente diversi da quelli utilizzati nel paragrafo precedente. L’indagine così non può non continuare con dei dati che riportano le reali Elo dei giocatori. Come campione è stato scelto quello dell’11 settembre 2017 (dato a caso). Qui si scopre che il numero 1 ha un Elo di 1947 punti, ben lontano dai 3000 ipotizzati. Il 128° invece con i suoi 1438 sembra essere un po’ più vicino all’idea “medium player” che ha Elo 1500. È facile intuire che il prossimo passaggio sarà quello di rifare gli stessi calcoli usando la nuova tabella. Inutile ripetere quando già detto, sintetizziamo in:

• Giocatore medio, Elo = 1560
• Giocatore 1T, Elo = 1477
• Giocatore 2T, Elo = 1561
• Giocatore 3T, Elo = 1673
• Giocatore 4T, Elo = 1739
• Giocatore QF, Elo = 1819
• Giocatore SF, Elo = 1930
• Giocatore F, Elo = 1947

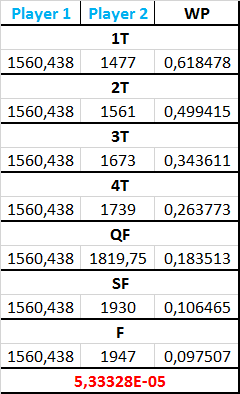
La ripetizione della simulazione dà i risultati riportati nella tabella. Essenziale è il numero evidenziato in rosso: 5,33 * 10 ^-5. L’omologo della simulazione precedente era 1.16 * 10^-9. Una riduzione di proporzione non indifferente (siamo nell’ordine di un fattore 45948).

Elo Real Masters

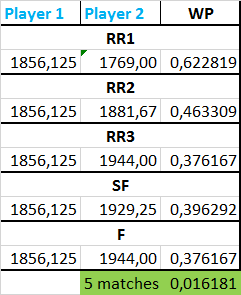
Simuliamo un Masters con i migliori 8 della classifica Elo reale dell’11 settembre 2017. Valgono tutte le considerazioni del paragrafo precedente. I risultati sono riportati nella tabella seguente:

La WP di vincere questo tipo di Masters è di 0,016181. La WP dell’altra simulazione 0.025457, ossia questo è circa il doppio più difficile. La proporzione tra WP(Slam) / WP(Masters) è uguale a = 303.4. Decisamente meno dell’altra proporzione. Però, per quanto minore, e di conseguenza un po’ vicina ai numeri che ci attenderemmo, un 303 è sempre troppo alto. Se applicassimo questa proporzione sostanzialmente si andrebbero ad annullare i punti proveniente dal Masters. Forse ci vuole un’altra via. Chissà quale è.